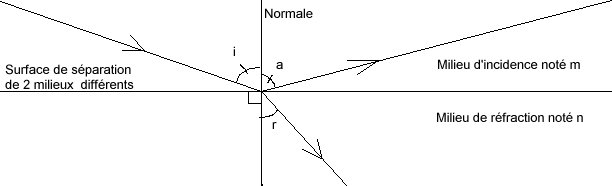
Légende :

N : Normale

i : Angle d'incidence

r : Angle de réfraction

a : Angle de réflexion

m : Milieu d'incidence

n : Milieu de réfraction

II Explication de la méthode

 

a) Quelques notions

La normale est la perpendiculaire à la surface de séparation de 2 milieux différents.

L'angle d'incidence est l'angle formé par le rayon lumineux avec la normale.

L'angle de réfraction est l'angle formé par le faisceau lumineux réfracté (après avoir traversé la surface de séparation) avec la normale.

L'angle de réflexion est l'angle formé par le faisceau lumineux réfléchi (après avoir été réfléchi sur la surface de séparation) avec la normale.

Ceci ne fonctionne qui s'il y a un changement de milieu !!!

b) Les lois de Descartes

1. L'angle d'incidence est égal à l'angle de réfraction.

2. Si la valeur du milieu de réfraction est supérieur à la valeur du milieu d'incidence alors l'angle de réfraction est plus petit que l'angle d'incidence.

3. Si la valeur du milieu de réfraction est supérieur à la valeur du milieu d'incidence alors l'angle de réfraction est plus petit que l'angle d'incidence.

4. m x Sin ( i ) = n x Sin ( r )

5. Le milieu d'incidence a pour valeur : m = ( n x Sin ( r ) ) / Sin ( i )

6. Le milieu de réfraction a pour valeur : n = ( m x Sin ( i ) ) / Sin ( r )

7. Quand l'angle d'incidence est égal à 0°, l'angle de réfraction est lui aussi égal à 0°.

c) Exemples

Donnée :

i = 60°

Calcul de a

i = 60°

L'angle d'incidence est égal à l'angle de réflexion.

Donc : i = a

i = a

Donc : a = 60°

Calcul de r par rapport à i

n = 1,3

m = 1,0

Donc : n > m

n > m

m x Sin ( i ) = n x Sin ( r )

Donc : Sin ( i ) > Sin ( r )

Calcul de r

n = 1,3

m = 1,0

i = 60°

m x Sin ( i ) = n x Sin ( r )

Sin ( r ) = m x Sin ( i ) / n

m = 1

Donc : Sin ( r ) = Sin ( i ) / n

Sin ( r ) = 0,666173387526491266741325515963797

r = 41,7724075665657771542725126215384°

r = 42°

L'angle de réfraction est d'environ 42°.

Calcul de m

i = 60°

r = 41,7724075665657771542725126215384°

n = 1,3

m x Sin ( i ) = n x Sin ( r )

m = n x Sin ( r ) / Sin ( i )

m = 1,0

La valeur de l'indice du milieu m est de 1,0.